Skip to contents

Check whether local factors are present and find the rotation of the loading matrix with the smallest l1-norm.

Source: R/local_factors.R
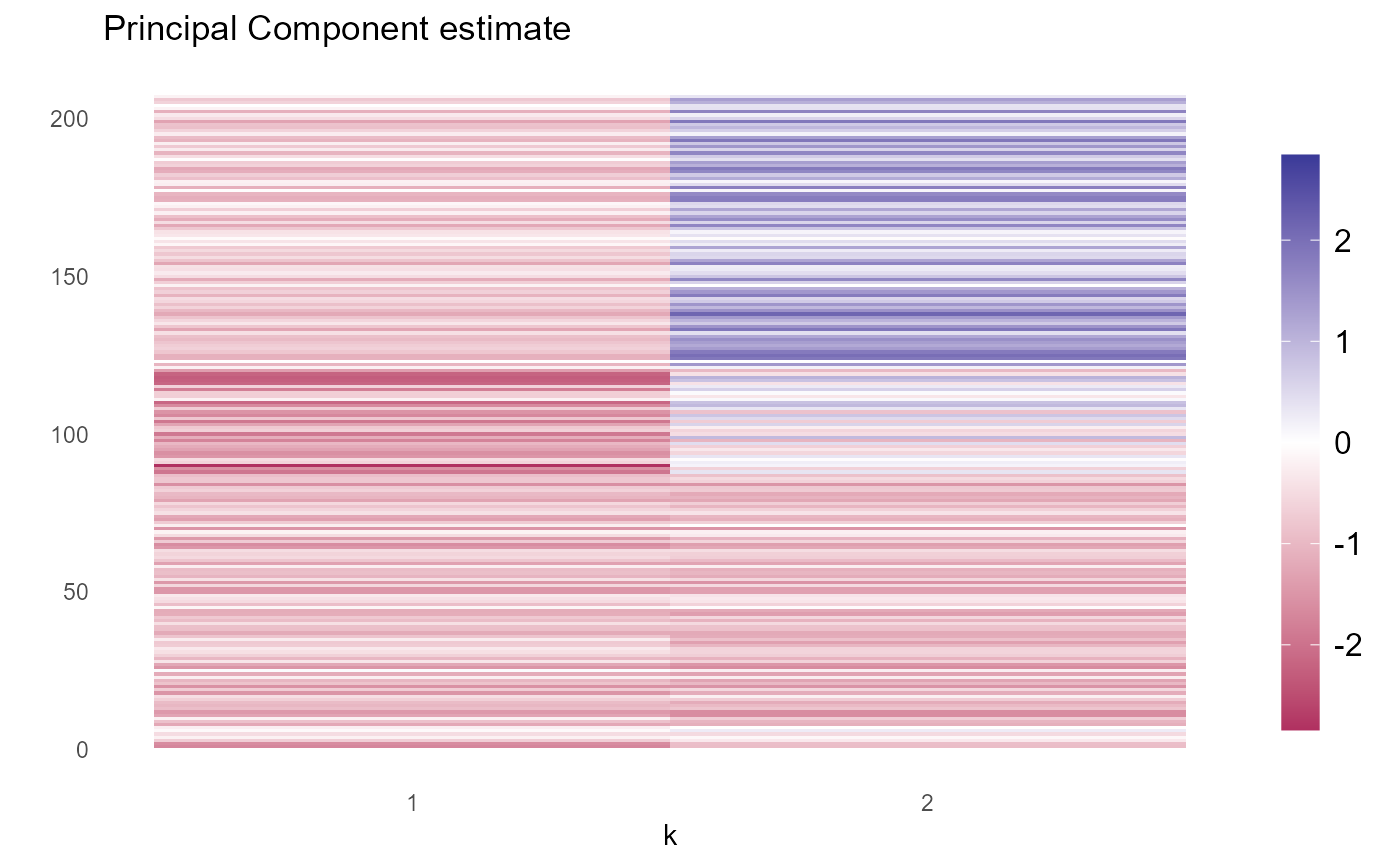
local_factors.Rd

local_factors tests whether local factors are present and returns both the Principal Component estimate of the loadings and the rotation of the loadings with the smallest l1-norm. It also produces graphical illustrations of the results.

Usage

local_factors(X, r, parallel = FALSE, n_cores = NULL)

Arguments

X

A (usually standardized) t by n matrix of observations.

r

An integer denoting the number of factors in X.

parallel

A logical denoting whether the algorithm should be run in parallel.

n_cores

An integer denoting how many cores should be used, if parallel == TRUE.

Value

Returns a list with the following components:

  • has_local_factors A logical equal to TRUE if local factors are present.

  • initial_loadings Principal component estimate of the loading matrix.

  • rotated_loadings Matrix that is the rotation of the loading matrix that produces the smallest l1-norm.

  • rotation_diagnostics A list containing 3 components:

    • R Rotation matrix that when used to rotate initial_loadings produces the smallest l1-norm.

    • l1_norm Vector of length r containing the value of the l1 norm each solution generates.

    • sol_frequency Vector of length r containing the frequency in the initial grid of each solution.

  • pc_plot Tile plot of the Principal Component estimate of the loading matrix.

  • rotated_plot Tile plot of the l1-rotation of the loading matrix estimate.

  • small_loadings_plot Plot of the number of small loadings for each column of the l1-rotation of the loading matrix estimate.

Examples

# Minimal example with 2 factors, where X is a 224 by 207 matrix
lf <- local_factors(X = example_data, r = 2)

# Visualize Principal Component estimate of the loadings
lf$pc_plot


# Visualize l1-rotation loadings
lf$pc_rotated_plot
#> NULL